Maschinelle Intelligenz für Asset-Allokation und Portfoliokonstruktion

Maschinelle Intelligenz ist heute in der Lage, komplexe ­Zusammenhänge in Kapitalmarktportfolios zuverlässig zu erfassen und in die Portfoliokon­struktion und -steuerung zu integrieren. Es werden ­robustere ­Ergebnisse als mit den traditionellen Ansätzen nach Markowitz und Risk Parity erzielt. Das liegt an einer neuen ­Qualität im Diversifikations- und Risikomanagementprozess. Zudem lassen sich effiziente, zunehmend digitalisierte Investmentprozesse realisieren. Dies gilt zum Beispiel für Aktien- und Multi-Asset-Port­folios im ­Bereich Smart Beta, Faktor-Investing und ESG.  

Künstliche Intelligenz verbreitet sich derzeit rasant in allen mög­lichen Wirtschaftsbereichen. Wir steuern auf die „AI Economy“ zu. Es wird sehr viel über die Potenziale geschrieben, doch machen wir uns nichts vor: Sie steckt noch in den Kinderschuhen und ist weit entfernt davon, beliebige Probleme zu lösen. Zudem stellt sich die Frage, ob unsere Gesellschaft dies überhaupt angemessen auf rechtlicher, sozialer­ und ethischer Ebene integrieren kann. Unabhängig davon gibt es aber Aufgaben im Investmentprozess, die heute zuverlässig und ­effizient von maschineller Intelligenz unterstützt werden können und den Investor oder Portfoliomanager mit neuen Möglichkeiten ausstatten. Liegen zum Beispiel strukturierte Daten wie Bilanzen oder Kurszeitreihen vor, so kann die Maschine diese schnell und zuverlässig auswerten – oft besser als der Mensch. Die Maschine kann dem Menschen also punktuell helfen.

Gerade bei der Auswertung von Kurszeitreihen tun sich viele traditionelle Methoden schwer. Es kommen immer noch viele lineare ­Modelle wie Regressionen oder Varianten nach Markowitz zum Einsatz, die schlicht nicht in der Lage sind, die überlinearen komplexen Dynamiken der Finanzmärkte zu erfassen. Die Märkte werden durch ­zunehmende Globalisierung und Informationsverarbeitung immer vernetzter. Auch die koordinierten Zentralbankeingriffe seit der ­Finanzkrise führen zu einer zusätzlichen Gleichschaltung der Marktbewegungen, was schnell zu Ansteckungseffekten oder „Butterfly ­Defects“ führen kann.
Diese überlagernden und dominierenden Effekte­ werden in den meisten Ansätzen, wie zum Beispiel Risk ­Parity, entweder gar nicht berücksichtigt oder nur unzureichend adressiert wie zum Beispiel im Varianz-/Kovarianzansatz. Die Finanzökonomie versucht immer noch zu beschreiben, wie sich die Märkte verhalten „sollten“. Dabei können intelligente Methoden der Datenverarbeitung erfassen, wie die komplexen Strukturen und Marktdynamiken ­„gerade beschaffen sind und wohin sie sich verändern“.

Diese Methoden ­basieren auf maschineller Intelligenz und finden prägnante Strukturen in den Daten, die die Komplexität der ­Dynamiken direkt erfassen und steuerbar machen, wobei keine problematischen Annahmen, wie zum Beispiel Linearität oder Normalverteilung, ­getroffen werden müssen.Bereits im Juli 2013 und Januar 2014 hatten wir in portfolio institutionell hierüber berichtet und konkrete Anwendungsbeispiele diskutiert.Mittlerweile haben diese Finanztech­nologien ihre Verbreitung rasant fortgesetzt und werden aktuell zum Beispiel in mehreren Beiträgen im Journal of Portfolio Management diskutiert.
Auch hier kommt man unabhängig zu demselben Ergebnis: Maschinell unterstützte Ansätze überbieten die traditionellen Methoden, was die Robustheit der Outperformance, also deren Out-of-sample-­Güte, angeht. Es gibt bereits einige Investmenthäuser, die schon ­einen überzeugenden Track Record aufbauen konnten. Die neuen Methoden scheinen zu funktionieren und das über eine ganze Palette an ­Anwendungen und Investmentprodukten hinweg.

Die Idee hinter dem maschinellen Ansatz ist, die ineinander verschachtelten Abhängigkeitsstrukturen der Assets aus den Kurszeit­reihen zu extrahieren und somit ein Bild zu bekommen, wie vernetzt und gruppiert sich die Assets verhalten – auch dynamisch im Zeitablauf. Schon Nobelpreisträger Herbert Simon wies darauf hin, dass komplexe Daten eine hierarchische, vernetzte Struktur auf­weisen. ­Finanzmärkte sind zweifelsohne komplex, so dass diese Aussage insbesondere hier ihre Gültigkeit hat.
Die gängigen Top-down-Ansätze der Asset-Allokation und Portfoliokonstruktion berücksichtigen diese Hierarchie oft schon implizit: So wird Risk Parity zum Beispiel auf Ebene natürlicher Gruppierungen wie Asset-Klassen/Industrien/­Regionen und dann nochmal innerhalb der Gruppen ­angewendet. Das Problem ist aber, dass die Gruppen sich heute ­wegen der Vernetzung stark durchmischen und dass auch innerhalb der Gruppen komplexe Abhängigkeiten zu finden sind.
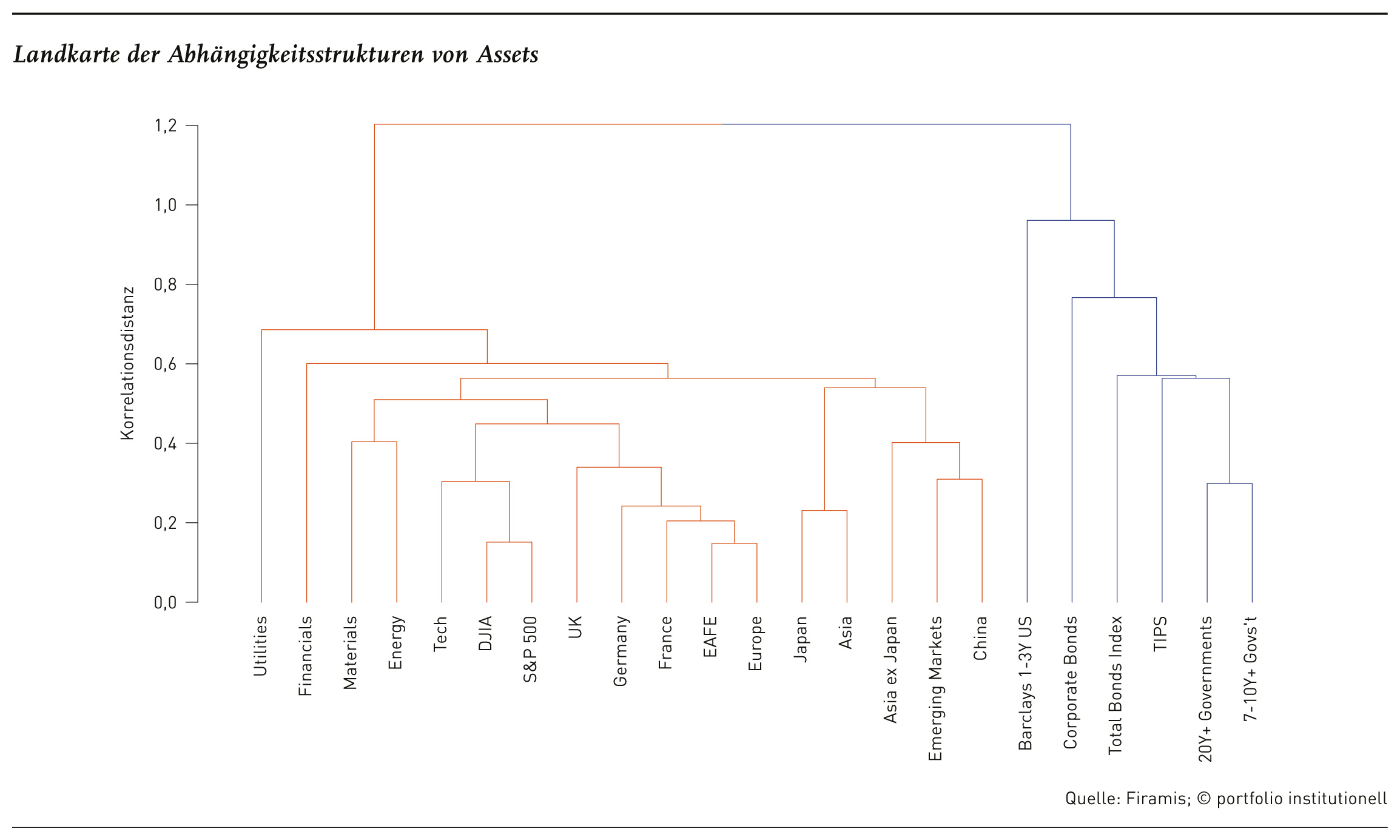
Zudem kann es oberhalb der Gruppen noch sogenannte Meta-Gruppen geben. Man braucht also ­eine hierarchische Landkarte der Gruppierung, die die volle Struktur von der Spitze bis zur unteren Ebene der Einzel-Assets anzeigt, um die Zusammenhänge wirklich zu verstehen. Das leistet die Maschine, die diese Struktur für jedes Portfolio beziehungsweise Universum aus den Daten extrahiert. Das Beispiel unten nutzt die Kurszeit­reihen ­einiger viel gehandelter ETF, die Aktien und Bonds sowie ­verschiedene Industrien, Regionen und Qualitäten abdecken. Die hierarchische Struktur wurde aus den Daten ohne weiteres Zutun „gelernt“:

Der linke Ast enthält die Aktien-ETF und der rechte die Bond-ETF. Darunter setzt sich die hierarchische Struktur fort. Bei Indizes oder Einzelinvestments ergeben sich ähnliche Strukturen. Das Bild (Dendrogram) erinnert stark an einen evolutionären Baum, wie man ihn aus der Biologie zur Klassifizierung von Tierarten kennt. In der Tat ­nutzen Natur- und Computerwissenschaften diese Art der Netzwerkmodellierung schon seit Jahrzehnten erfolgreich, um komplexe Systeme der Natur und Technik besser zu verstehen. Googles Herzstück zur ­Suche relevanter Web-Inhalte zum Beispiel ist ein Graph-Ansatz. Soziale Plattformen wie Facebook oder Linkedin wären ohne Netzwerkanalytik nicht denkbar. Es ist Zeit, diese Methoden nun auch systematisch im Asset Management einzusetzen. 
Nun diskutieren wir einige konkrete ­Anwendungsszenarien. Wir bleiben zunächst bei den ETF und simulieren eine Reihe von Portfolios, die mit der Netzwerkmethode ­konstruiert werden. Wir integrieren die Netzwerkstruktur dabei in ­einen risiko- und diversifikationsbasierten Long-only-Investment­ansatz, der ohne Renditeprognosen auskommt. Die Portfolios variieren dabei in ihrem Verhältnis zwischen Aktien- und Bondanteil je nach Risikoneigung des Kunden. Genutzt werden hier alle Kombinationen, zusätzlich wird mit unterschiedlichen Rebalancierungsschritten gearbeitet (jährlich und quartalsweise).
Somit entsteht eine große Menge möglicher Portfolios und Strategien, die Kunden zum Beispiel auf einer typischen Robo-Advisory-Plattform anfragen können. Von Interesse ist nun, welche Performance all ­diese Strategien aufweisen. Dazu errechnen wir die Ergebnisse über ­längere Zeiträume inklusive der globalen Finanzkrise und mitteln diese über alle Strategien. Dasselbe tun wir auch mit den traditionellen Vergleichsansätzen und erhalten folgendes Sharpe Ratio: Graph-Ansatz 0.82, Minimum Varianz 0.73 und Risk Parity 0.64.

Die Graph-Methodik schneidet besser ab, obwohl auch diesem Ansatz nur die traditionelle Varianz-/Kovarianzmatrix übergeben wurde, um dieselbe Ausgangsinformation wie bei Minimum Varianz und Risk Parity herzustellen. Der Graph-Ansatz zeigt hier also noch gar nicht sein ganzes Potenzial. Dies ist sicherlich nur ein einfacher Test, ­jedoch unter praxisnahen Einsatzbedingungen bei einem Robo Advisor. Ähnlich gute Ergebnisse werden auch bei den Downside-Risiken erzielt, wie die sogenannte Pain Ratio zeigt. Diese setzt den ­erzielten Ertrag ins Verhältnis zu Länge und Tiefe von Drawdowns. Je höher die Erträge bei gleichzeitig geringen Drawdowns, desto größer die Kundenzufriedenheit. Auch hier zeigt sich die Dominanz des ­Graph-Ansatzes.

Probleme liegen darin, dass Risk Parity zu prozyklisch ist und sich schlechter von Drawdowns erholen kann. Nach einem Drawdown steigen Korrelationen und Volas an, und genau dann arbeitet Risk ­Parity mit zu wenig Allokation in Märkten mit gestiegener Volatilität. Genau diese Märkte haben aber die höchste Erholungschance. Das Minimum-Varianz-Portfolio konzentriert sich meist in wenige Werte mit geringer Volatilität und verpasst breite Markter­holungen. Der risikoreduzierende Graph-Ansatz erzeugt geringe Draw­downs, trägt aber gleichzeit dafür Sorge, möglichst breit über die Märkte zu streuen.
Damit partizipiert er an starken Erholungen. Vergleichbar gute Ergebnisse werden auch auf anderen Datensätzen mit einer oder mehreren Asset-Klassen sowie auch für weit größere Portfolios erzielt. Zudem wurden Portfolios auf Basis ­simulierter, künstlicher Datensätze mit ähnlich guten Ergebnissen generiert. Dies zeigt die Generalisierungsfähigkeit des Ansatzes und dessen Stabilität out of sample. Es handelt sich demnach um eine echte Querschnitttechnologie, die sich für ­eine Vielzahl an Strategie­varianten und Investmentprodukten eignet.

Eine andere Studie untersucht, wie die Vernetztheit in Portfolios als alternatives Konzept für die aktive Steuerung eines Multi-Asset-Klassen-Portfolios genutzt werden kann – sowohl rein risikobasiert als auch risiko/ertragsbasiert. Auch hier dominiert der Graph-Ansatz die konventionellen Ansätze. Eine weitere Studie bezüglich Aktien­portfolios zieht neben der Vernetzungsinformation weitere typische Faktoren wie Volatilität und Momentum hinzu. Es wird eine Outperformance erzielt und es kann gezeigt werden, dass die Graph-Struktur unkorreliert zu diesen Faktoren ist und eigenes Alpha produziert (der Netzwerk-Diversifikationsertrag).

Die Kombination der Graph-Ansätze mit bestehenden Views, Marktmeinungen, Styles und (Trend-)Schätzern aus quantitativen oder ­diskretionären Ansätzen ist ebenfalls möglich. Hierbei wird der ­Maschine ein anderes Lernprogramm vorgelegt, das das Portfolio nach den bekannten Metriken und Leitplanken ausrichtet und zusätzlich durch die Graph-Komponente erweitert. Ein Beispiel ist die ­Maximierung der erwarteten Renditen bei gleichzeitiger Kontrolle der Netzwerkdiversifikation. Letzeres stabilisiert die Unsicherheit der ­Ertragsprognosen und führt zu robusteren Ergebnissen. Ein anderes Beispiel aus der ESG-Welt: Durch die Selektion von Assets mit guten ESG-Werten reduziert sich die Portfoliogröße und es sammelt sich ­eine Reihe hochkorrelierter Assets.
Zwar ist das Einzelrisiko dieser Assets insbesondere aufgrund der guten ESG-Werten ­reduziert, die geringe Anzahl an Titeln und deren starke Korrelation bleiben ­jedoch bestehen. Hier kann der Graph-Ansatz dafür sorgen, diese ­negativen Eigenschaften besser abzumildern als mit herkömmlichen Methoden. Auch bei alternativen Indizes hilft der Graph­-Ansatz. Hier werden oft Assets untergewichtet, die stark korreliert ­zueinander sind, um eine diversifizierte Basis zu haben für weitere Filterregeln gemäß Risiko, Dividende et cetera. Auch hier leistet der Graph- bessere Dienste als der einfache Korrelationsansatz. Beim faktorbasierten Investieren tritt oft das Problem auf, dass die Faktoren und/oder Styles nicht rein genug sind und Tilts aufweisen. Sie korrelieren stärker als gedacht und dieses Problem kann mit dem Graph-Ansatz gemildert werden, wenn genügend Zeitreihen vorliegen und die Graph-basierte Faktor­diversifikation in investierbare Portfolios übersetzt werden kann.

Zum Abschluss diskutieren wir das Potenzial des Graph-Ansatzes für automatisierte Investmentdienstleistungen und im Bereich der ­Digitalisierung. Der Graph-Ansatz ist Teil eines systematischen, regel­basierten und computergestützten Investmentprozesses und trägt ­somit zur weiteren Digitalisierung bei. Die gelernten Portfoliostrukturen sowie die darauf basierenden Handlungsempfehlungen können mit entsprechenden Algorithmen visualisiert werden, um intuitives Verständnis der komplexen Portfoliodynamik sowie entsprechende Wirkmechanismen des maschinellen Lernens transparent zu machen. Die Investoren erhalten somit eine größere Transparenz. Diese Dokumentationen können auch für regulatorische Anforderungen (Konsumentenschutz, Risikomanagement) verwendet werden.
Zudem können die Investoren Extraleistungen beziehen, indem ihr Portfolio ­einer automatischen Dauerüberwachung unterstellt wird, um Verwerfungen und Risikokonzentrationen frühzeitig zu identifizieren und zeitnah wirksame Heilungsschritte vorzuschlagen. Das ETF-Beispiel hat gezeigt, dass die Methode robuste Ergebnisse für eine ganze ­Reihe spezifischer Portfolios bietet. Im Idealfall erhält der Investor sein ­individuelles robustes Portfolio, ohne aus einer Menge an vorgefertigten Produkten wählen zu müssen – ein weiterer Schritt in Richtung Digitalisierung und Nutzung von Finanztechnologie (Fintech).

portfolio institutionell, Ausgabe 02/2017

• Investoren: Technologien werden Branche umwälzen
• Mit Netzen fängt man nun auch Mäuse
• Netzwerke sind mehr als Vitamin B